Deformazioni canne in Carbonio al limite dell'utilizzo
- Dettagli
- Categoria principale: Fly Fishing Magazine
- Categoria: Sotto la lente
- Scritto da Matteo Fongaro (matteof)
Deformazione e stati di tensione
delle canne in carbonio al limite dell' utilizzo
di Matteo Fongaro (matteof)
delle canne in carbonio al limite dell' utilizzo
di Matteo Fongaro (matteof)
Utilizzando una canna da mosca, quando la coda in volteggio raggiunge una distanza rilevante, particolare per quella canna, un abile lanciatore che tenti di andare oltre può avvertire una sorta di "cedimento" della stessa, situazione che viene rappresentata con frasi tipo "la canna si siede" o "si inginocchia" o "è sorda". Qualcuno avverte pure un "riprendersi" della canna oltrepassata questa distanza. Da una discussione sul Forum è scaturito l'impegno, concretizzatosi in questo articolo, dell'amico Matteo Fongaro (matteof) ad andare più a fondo nell'esaminare cosa capita quando una canna è usata intorno al limite delle sue prestazioni
Voglio innanzitutto mettere le mani avanti e spiegare i motivi che mi spingono a scrivere di questi argomenti e di conseguenza gli obiettivi che mi pongo nel pensare e scrivere in linguaggio matematico.
La prima considerazione che mi sorge spontaneo fare, è che non ho scritto le tavole della legge, né ho la presunzione di ritenere che quello che scrivo si assolutamente corretto anzi, mi sono messo nella posizione di uno che ha delle conoscenze tecniche (di fisica e matematica) superiore alla media e tenta di dare una interpretazione a certi fenomeni.
È ovvio che un ingegnere dei materiali laureato con 110 e lode alla Normale di Pisa, con un master in tecnologie dei materiali aerospaziali allo Space Center Americano ne sa più di me, e magari quello che scrivo lo trova scorretto o incompleto, ben venga. Io adoro imparare e penso che, chi mi corregge mi insegna, se poi mi corregge una cosa giusta, io avrò imparato comunque.
Quindi il mio invito è di leggere il tutto con un ampio occhio critico e di farmi presente ogni cosa che non vi torna di modo tale che questo non sia un punto di arrivo, ma di partenza per future e più profonde considerazioni.
Per una mia predisposizione, quando gli argomenti si fanno tosti e difficili da seguire, ci inserisco delle battutine, delle stupidaggini solo per sdrammatizzare e per alleggerire il discorso, non me ne abbiate.
Prima di iniziare a teorizzare delle formule occorre necessariamente sapere di cosa stiamo parlando. Il carbonio, elemento essenziale per la costruzione delle canne da pesca, è l’elemento chimico contrassegnato dalla lettera C, cosa importante è un non metallo, quindi ha le proprietà fisiche e chimiche dei non metalli.
Altra considerazione importante da fare è che il carbonio può avere, a seconda della configurazione degli orbitali atomici (paroloni complicati ma credetemi che è così sulla fiducia), legami con 4 o 3 o 2 atomi. Questo è molto importante perché a seconda di quanti atomi si sono combinati con il carbonio avremo molecole di materiali diversi, con diverse caratteristiche fisiche e chimiche. Importantissimo poi è sottolineare che non tutti i legami atomici sono uguali e a seconda del tipo e del numero di legami avremo materiali più o meno duri e resistenti (non scendo nel dettaglio perché solo di questo si dovrebbe scrivere un libro).
Esistono perciò una grandissima varietà di composti del carbonio, che tra l’altro si lega benissimo con molti altri elementi come l’ossigeno( ) e l’idrogeno (
) e l’idrogeno ( un tipo di zucchero), ovviamente la parte di applicazione del carbonio che interessa a noi è quella strettamente legata al materiale come elemento costruttivo delle canne da pesca, che nello specifico è la grafite.
un tipo di zucchero), ovviamente la parte di applicazione del carbonio che interessa a noi è quella strettamente legata al materiale come elemento costruttivo delle canne da pesca, che nello specifico è la grafite.
In natura la grafite ha due configurazioni la cosiddetta alfa e beta, la prima ha una struttura esagonale, la seconda romboidale, nelle grafite industriali si riscontrano solo le strutture alfa. La grafite ha la caratteristica di essere formata da più fogli di atomi che sono separati da diversi altri atomi che, nel caso funzionino da collante, hanno strutture e forze tali da tenere attaccati i fogli, gli stessi hanno la tendenza a scivolare gli uni sugli altri.
Avete mai notato in caso di rottura di una canna da pesca, sembra che si squami perdendo via via pezzetti sottili di materiale che si sfalda. Ovviamente bisogna considerare che l’industria ha messo a punto sistemi di trattamento meccanico in grado di variare la struttura della grafite (da alfa a beta) e l’aggiunta di altri elementi di rinforzo come il Kevlar consente di avere materiali con diverse caratteristiche meccaniche. Classificare e stabilire per tutte le strutture a base di carbonio utilizzate per la pesca, le caratteristiche fisiche è una utopia perché molti materiali sono coperti da brevetti e la varietà è tale da rendere l’impresa ardua.
Per capire meglio il discorso, per la verità un po’ complicato che andremo a fare di seguito dobbiamo porre alcuni punti saldi da cui iniziare. Prendiamo un elemento di materiale, nel nostro caso una sezione di canna da pesca, poniamo come la lunghezza inziale a riposo dell’elemento campione l sarà invece la lunghezza modificata a causa delle tensioni ora definiamo come:
la lunghezza inziale a riposo dell’elemento campione l sarà invece la lunghezza modificata a causa delle tensioni ora definiamo come:
Allungamento: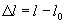
Deformazione lineare epsilonE (teorica):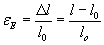
Deformazione lineare epsilonT (reale):
dove ln è logaritmo naturale base e (per chi vuole approfondire l’argomento logaritmi per capire meglio mi scriva pure).
Bisogna inoltre porre in chiaro un concetto: sforzi e deformazioni dipendono inequivocabilmente dal materiale ma sono assolutamente indipendenti dalla forma in cui sono costruiti. Quindi uno studio su una fibra lineare di carbonio permette di avere risultati paragonabili e assimilabili per una canna da pesca oppure per l’alettone di una formula uno.
Una canna da pesca ha la sezione circolare, prendiamo come approssimazione che tale non abbia spina, e che sia perfettamente rotonda.
Prendiamo un elemento della canna:
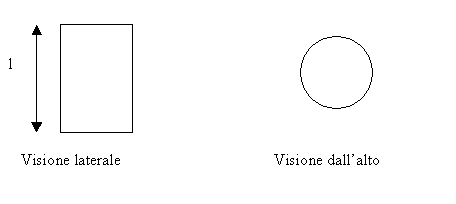
Durante le sollecitazione dovute al lancio la struttura si deforma
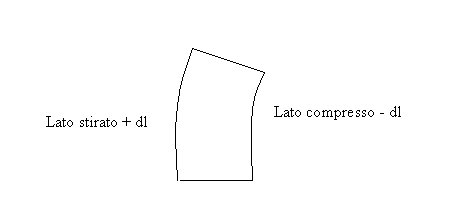
Un lato subisce uno stiramento e la sua lunghezza aumenta di +dl, mentre dall’altra parte il lato subisce una compressione e la sua lunghezza diminuisce di un –dl. Nello specifico selezionando un elemento da entrambi i lati avremo questa situazione:
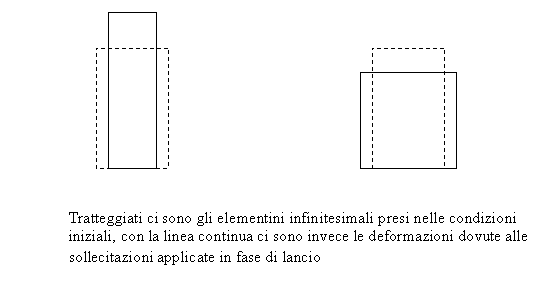
Ora che abbiamo posto le basi per il nostro studio possiamo immaginare di mettere il nostro campione in una speciale macchina che provvederà a mettere in tensione il materiale, questo ci permetterà di studiare il comportamento del materiale sotto tensione nel lato in cui avviene lo stiramento. Come detto in precedenza lo sforzo e la deformazione sono indipendenti dalla forma del materiale e quindi possiamo studiare la fibra lineare che viene messa in trazione da uno sforzo progressivo e quindi si stira.

Nel grafico Y è il valore della massima tensione ammissibile prima di passare al comportamento plastico. A0 è l’area iniziale della sezione del nostro elemento.
Interpretando il grafico sopra illustrato abbiamo i vari stadi in cui possiamo dividere il materiale durante la prova di tensione.
1) il materiale si allunga all’interno del range di valori in cui ha deformazioni elastiche interrompendo la tensione il materiale torna al suo originale stadio.
2) Passando al di là della soglia di plasticità il materiale continua ad allungarsi in modo uniforme, senza cioè subire significative variazioni di volume. Nello specifico, interrompendo la tensione il materiale tornerebbe alla sua posizione iniziale avendo però delle deformazioni plastiche mantenendo comunque un comportamento elastico
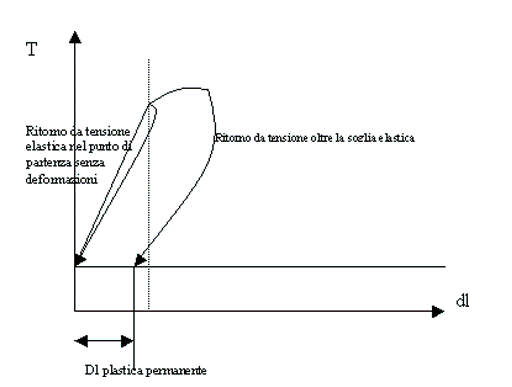
3) proseguendo oltre con la tensione il materiale viene stirato e in un punto, solitamente verso il centro, il materiale forma un collo in cui c’è variazione di superficie dell’area considerata. In questo punto il materiale, analogamente al punto 2 ha un comportamento elastico ma deformazioni plastiche. Importante è notare che, sia nella fase 2 che nella 3, in rapporto alla tensione applicata all’inizio, basta un lieve aumento della tensione stessa per provocare significative deformazioni. Nell’applicazione pratica della pesca, la canna quando raggiunge il limite della tensione elastica/plastica, la canna non ha praticamente deformazioni (vedremo in seguito si dice comportamento anelastico), superando il limite, cioè allungando il lancio e aumentando le forze in azioni, la canna ha deformazioni sensibili anche con leggeri aumenti (da 20 a 21 mt di coda per intenderci).
Altra considerazione da fare su questa fase è che il materiale, come si evince dalla cupside del grafico ha un punto di massimo, tale rappresenta la massima tensione sopportabile dal materiale; per materiali fragili in questo punto si ha rottura, per i materiali duttili vi è la diminuzione della sezione già descritta in precedenza.
4) Proseguendo ancora c’è la rottura che avviene sempre nella zona del materiale che ha subito lo stiramento con la conseguente variazione di area.
Ultima considerazione sul grafico della ipotetica prova è che i materiali hanno un comportamento elastico lineare entro particolari range di deformazioni, ed assumere comportamenti non lineari per valori più elevati. Ovviamente si possono studiare le deformazioni e le tensioni nel campo lineare, quando non sussiste più la linearità delle deformazioni entrano in campo altre variabili (la composizione del materiale, la temperatura, il tempo di esposizione alla tensione) ed è praticamente impossibile determinare il comportamento se non al limite per materiali puri.
Andiamo ora a condire le considerazioni con un po’ di matematica e fisica per capire effettivamente come e dove succedono le cose appena descritte
Ricapitolando brevemente dobbiamo andare a studiare quelle che sono le deformazioni dovute alle sollecitazioni che per semplicità di comprensione andremo ad assumere infinitesimali andando a studiare un allungamento rettilineo.
Dobbiamo inoltre porre anche altre condizione a contorno:
1) definiamo come solido elastico un elemento che ha la capacità di riacquistare la sua forma iniziale appena scompaiono le forze applicate
2) immaginiamo di avere una tensione uniforme e distribuita uniformemente
La tensione applicata T=F/A cioè la forza su unità di area e la deformazione come cioè il rapporto tra l’allungamento misurato e la lunghezza originaria.
cioè il rapporto tra l’allungamento misurato e la lunghezza originaria.
Da qui possiamo arrivare a formulare semplicemente che:
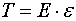
dove T è la forza applicata E è la costante di proporzionalità, che nel mondo intero è conosciuta come modulo di Young (ne parleremo dopo), mentre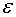 è la deformazione.
è la deformazione.
A seconda del materiale e quindi del relativo modulo di Young possiamo stabile la T limite per la deformazione, tale rappresenta nella pratica la soglia oltre cui il comportamento non è più elastica.
Per dare un’idea il modulo di Young per le fibre di carbonio è compresa tra i 275 e i 415 Gpa, per la fibra di vetro è tra i 73 e gli 85 Gpa, per l’acciaio è tra 190 e 200 Gpa, il diamante ha un modulo di Young tra gli 820 e i 1050 Gpa.
Abbiamo quindi definito T, cioè il limite elastico, oltre a questo limite si nota comunque un incremento della deformazione anche senza aumento della tensione ed è il cosiddetto limite di snervamento. Crescendo ulteriormente si notano deformazioni significative fino al limite di rottura e la conseguente rottura del campione.
Ora lo studio del comportamento meccanico dei solidi elastici ha animato i sogni di parecchi matematici e fisici dal XXVII secolo ed in particolare di un fisico/matematico di nome HOOKE che suggerì una generalizzazione proposta già precedentemente da CAUCHY. La differenza sostanziale tra i due era che Hooke conduceva una vita ben più animata, amava infatti il bere il mangiare e soprattutto le donne e questa spensieratezza lo rendeva un pelino più brillante per quei tempi soprattutto per quanto concerne le applicazioni pratiche della sue intuizioni. Cauchy invece faceva una vita triste, e quindi era un grande astrattista specie nella matematica ma quanto al resto pare non avesse successo con le donne e quindi era attanagliato da una grande miopia.
Hooke propose la seguente generalizzazione partendo da una serie di assiomi:
1) lo stato di tensione è funzione univoca dello stato di deformazione, il che si traduce in:

2) le componeti di tensione T si annullano identicamente se sono nulle tutte le componenti di deformazione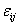 il che implica che nelle condizioni iniziali non è soggetto alcuno stato di tensione
il che implica che nelle condizioni iniziali non è soggetto alcuno stato di tensione
3) la funzione f non dipendono esplicitamente dalla posizione x, quindi in materiale è omogeneamente elastico cioè in ogni punto l’elasticità è la stessa
4) il legame dove (i,j,k,l=1,2,3) è un legame lineare.
dove (i,j,k,l=1,2,3) è un legame lineare.
Ora, la combinazione dei coefficienti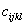 sono 3 alla quarta e quindi 81, risparmiandovi la dimostrazione fidatevi se vi dico che nella realtà ne bastano 36 se si tiene conto della simmetria del tensore T, fidatevi inoltre se vi dico che si riducono ulteriormente a 21 se parliamo di un solido omogeneo anisotropo.
sono 3 alla quarta e quindi 81, risparmiandovi la dimostrazione fidatevi se vi dico che nella realtà ne bastano 36 se si tiene conto della simmetria del tensore T, fidatevi inoltre se vi dico che si riducono ulteriormente a 21 se parliamo di un solido omogeneo anisotropo.
Quindi dovremmo in pratica conoscere 21 costanti elastiche (c) per definire 6 tensori di sforzo in grado di descrivere il comportamento elastico, vi scrivo solo il primo:
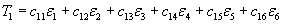
Quindi si andranno di seguito a costruire 6 tensori, da 1 a 6 in cui saranno considerate tutte le costanti elastiche dei vari punti per le relative deformazioni epsilon.
La domanda che sorge spontanea è perché 6 tensori? Allora dobbiamo considerare di avere tre sforzi normali lungo gli assi x,y,z più tre sforzi di taglio xy,xz,yz, questi sei tensori ci danno la gamma completa degli sforzi applicabili.
Semplifichiamo un po’ le cose per renderle leggibili; quella che vi ho enunciato in precedenza è la legge di Hooke nella sua funzione generale e nel suo più ampio spettro di utilizzo. Ovviamente, per le nostre applicazioni non ha senso andare a studiare un numero di tensori così ampio ed andare alla ricerca sperimentale delle costanti elastiche, meglio applicare una ulteriore semplificazione introducendo la legge di Hooke coadiuvata dal modulo di Young.
Non vi dico niente sulla vita di Young, vi dico solo di non confonderlo con Paul Young che è un cantante degli anni ottanta tramontato ormai da tempo e conosciuto in Italia per un duetto con Zucchero nella reinterpretazione di “Senza una donna”.
Seriamente la legge di Hooke diventa molto semplicemente:
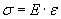
Tutta un’altra cosa,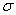 (sigma) è lo sforzo lungo un asse (lo chiamo così per evitare di confonderlo con il T che è un tensore visto in precedenza), E è la pendenza della linea di carico nella fase elastica vista in precedenza (punto 1) ed è caratteristica del materiale, indipendente dalla forma e vale per allungamento e compressione, è la deformazione.
(sigma) è lo sforzo lungo un asse (lo chiamo così per evitare di confonderlo con il T che è un tensore visto in precedenza), E è la pendenza della linea di carico nella fase elastica vista in precedenza (punto 1) ed è caratteristica del materiale, indipendente dalla forma e vale per allungamento e compressione, è la deformazione.
La deformazione al livello atomico è data da piccole variazioni della distanza interatomica, il modulo elastico E, o modulo di Young, altro non è che la misura della forza di legame ed è per questo che è strettamente dipendente dal tipo di materiale ed indipendente dalla forma: la prima è ovvia ogni materiale ha legami chimici propri e diversi e quindi resistenze di legame diverse, la seconda è altrettanto ovvia, a livello atomico che si parli di un canna da pesca o di un foglio di carbonio non si vede la differenza : sono atomi legati tra di loro.
Dobbiamo inserire un ulteriore elemento per riuscire poi a formulare una generalizzazione valida ed è il modulo di Poisson. Due parole su Poisson, francese, che nel 2006 non ha potuto vedere la sua nazionale campione del mondo per due motivi, il primo era già morto da un paio di secoli abbondanti, il secondo perche “siamo noi, siamo noi i campioni del mondo siamo noi”.
Poisson osserva giustamente che per la maggior parte dei materiali ad un allungamento dell’asse x a causa di una trazione corrisponde un aumento di volume. Nel caso di deformazione elastica questo è compensato da una contrazione laterale lungo y e z in perpendicolarità con x. Quindi:
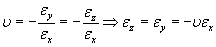
Tanto per dare due numeri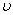 (upsilon = costante di Poisson) per le gomme vale 0,5, per i metalli 0,35 per i materiali ceramici 0.07-0.27. Applicandolo il modulo di Poisson per dedurre uno sforzo applicato lungo l’asse x avremo:
(upsilon = costante di Poisson) per le gomme vale 0,5, per i metalli 0,35 per i materiali ceramici 0.07-0.27. Applicandolo il modulo di Poisson per dedurre uno sforzo applicato lungo l’asse x avremo:

questo ci dà una relazione lineare tra sforzo applicato e deformazione laterale
Ora proviamo ad applicare questa semplificazione di Hooke, supponiamo un corpo sollecitato da un generico stato di sforzo, come abbiamo visto in precedenza per descrivere compiutamente il tutto dovremmo disporre di 6 equazioni, tre per gli assi e tre per gli sforzi di taglio. Consideriamo per semplicità i soli sforzi agenti lungo gli assi x, y e z, trascurando quelli di taglio.
L’applicazione di tali sforzi genererà anche una conseguente contrazione (Poisson) avremo quindi che la componente dello sforzo genera una
genera una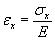 e le conseguenti deformazioni quantificabili con Poisson nelle direzioni y e z
e le conseguenti deformazioni quantificabili con Poisson nelle direzioni y e z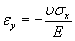 e
e 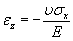 .
.
La stessa cosa ovviamente si avrà prendendo in considerazione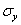 e
e  .
.
La deformazione totale lungo l’asse delle x sarà:

Quindi nei tre assi avremo le seguenti deformazioni:
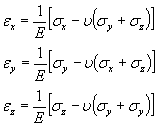
Come un miracolo della matematica abbiamo ridotto le equazioni a tre con due moduli elastici (dipendenti dal tipo di materiale) E e al posto di avere 6 equazioni con la bellezza di 36 costanti elastiche da calcolare (di cui solo 21 indipendenti).
al posto di avere 6 equazioni con la bellezza di 36 costanti elastiche da calcolare (di cui solo 21 indipendenti).
Questo ci permette di calcolare puntualmente le deformazioni che si osservano in ciascuna direzione per uno sforzo assegnato
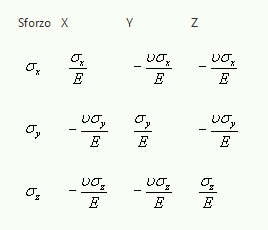
Ora facciamo il punto della situazione, abbiamo capito che i materiali danno diverse risposte alle sollecitazioni, a seconda degli sforzi assegnati si hanno delle deformazioni che possiamo calcolare partendo dai moduli elastici. Tutto questo è valido solo nel campo delle forze entro cui si hanno deformazioni elastiche (nello specifico prima delle tensioni di snervamento).
Analizziamo adesso i casi in cui si ha un comportamento anelastico e non lineare. Per farlo dobbiamo per forza di cose fare un viaggio all’interno della struttura molecolare del materiale. Immaginiamo il materiale come un agglomerato ordinato di paline (gli atomi) legati gli uni agli altri da delle molle. La forza di ritrazione (cioè la forza per tornare alla posizione iniziale) è indotto dallo spostamento degli atomi.
Per materiali come metalli, ceramici, vetri e polimeri la forza di ritrazione deriva da piccoli spostamenti degli atomi dalla loro posizione di equilibrio. Questi materiali sono dotati di una grande forza di coesione e quindi la forza di ritrazione è alta, il modulo elastico pure e le deformazioni sono limitate e associate ad un significativo aumento dell’energia interna mentre la configurazione solida (il reticolo di palline con le molle) risulta sempre inalterata.
Negli elastomeri (polimeri plastici sia naturali, che sintetici con grandi capacità elastiche) la struttura tridimensionale assicura la reversibilità delle deformazioni perché a spostarsi sono segmenti di catena di elastomeri (con forza di ritrazione alta) mentre tra le catene c’è una bassa forza di ritrazione. In altre parole le catene molecolari degli elastomeri sono dure e rigide ma tra loro sono debolmente legati. Esempio lampante di elastomero è la gomma, l’allungamento a trazione è molto ampio ma a muoversi non è il singolo atomo bensì la catena di atomi.
In alcuni casi possono osservare comportamenti anelastici, cioè la risposta del materiale in fase di carico e scarico non è lineare. Nella deformazione elastica ideale l’energia immagazzinata viene totalmente recuperata alla rimozione del carico, nel caso di comportamento anelastico una parte dell’energia di deformazione viene dissipata nel materiale attraverso meccanismi di attrito interno che si traduce in un movimento di dislocazione delle catene molecolari. La curva di scarico non è più uguale a quella di carico anche se il campione riassume la forma iniziale. Il comportamento anelastico si manifesta come una dipendenza elastica dal tempo che può essere osservata applicando uno sforzo costante ad un provino per un certo tempo e osservando come varia la deformazione nel tempo.
Tanto per citare due esempi di materiale con conclamato e visibile comportamento anelastico abbiamo la ghisa grigia, in cui l’effetto anelastico è dovuto ai movimenti di dislocazione delle lamelle di grafite inserite nella matrice di ferro, altro esempio sono i pneumatici, formati essenzialmente da elastomeri che rispondono alle tensioni con un attrito interno. Importante è notare che questi due materiali sono dei grandissimi ammortizzatori di vibrazioni.
In conclusione, tiriamo le somme definitive di questo lungo e complesso discorso cercando di capire cosa succede in una canna da pesca. Le canne da PAM, vendono sottoposte a continue sollecitazioni in tutti e tre gli assi. Con le formule che abbiamo visto possiamo determinare a priori (a patto ci conoscere le caratteristiche meccaniche dello specifico materiale composito) la tensione massima applicabile prima di raggiungere lo snervamento, le deformazioni sui tre assi attese a seconda delle forze applicate in modo abbastanza semplice.
Abbiamo inoltre visto che i materiali possono avere un comportamento anelastico, cioè facendo un lancio particolarmente oneroso in termini di tensioni, la risposta della canna non è più elastica e quindi non restituisce l’energia applicata non lavorando. Quando questo capita siamo già oltre il livello di tensione di snervamento e quindi, aumentando ulteriormente avremo delle deformazioni maggiori anche applicando piccole differenze di tensione (ad esempio passando da 20 a 21 metri di coda in aria, la tensione applicata in più è poca ma le deformazioni saranno maggiori) queste restituiranno una maggiore energia tale da superare il comportamento anelastico. Questo succede perché le catene molecolari che compongono il materiale si dislocano cercando una nuova dimensione spaziale perché nelle catene c’è una grande forza di coesione ma tra di loro le catene non sono legate da una grande forza.
Quindi questo spiega il comportamento sordo di certe canne in particolari stati di deformazione.
Non ho scoperto niente, né ho inventato o teorizzato qualcosa di nuovo, ho solo raccolto le nozioni necessarie e cercato di tradurle in un modo comprensibile e tale da fornire una spiegazione spero esauriente. Se avete notato qualche errore o omissione scrivetemi, se vi sembra che abbia scritto cose sbagliate scrivetemi saranno tutte ben accette.
Albano Barbiani (Ghost)
NOTA DELL’AUTORE
Voglio innanzitutto mettere le mani avanti e spiegare i motivi che mi spingono a scrivere di questi argomenti e di conseguenza gli obiettivi che mi pongo nel pensare e scrivere in linguaggio matematico.
La prima considerazione che mi sorge spontaneo fare, è che non ho scritto le tavole della legge, né ho la presunzione di ritenere che quello che scrivo si assolutamente corretto anzi, mi sono messo nella posizione di uno che ha delle conoscenze tecniche (di fisica e matematica) superiore alla media e tenta di dare una interpretazione a certi fenomeni.
È ovvio che un ingegnere dei materiali laureato con 110 e lode alla Normale di Pisa, con un master in tecnologie dei materiali aerospaziali allo Space Center Americano ne sa più di me, e magari quello che scrivo lo trova scorretto o incompleto, ben venga. Io adoro imparare e penso che, chi mi corregge mi insegna, se poi mi corregge una cosa giusta, io avrò imparato comunque.
Quindi il mio invito è di leggere il tutto con un ampio occhio critico e di farmi presente ogni cosa che non vi torna di modo tale che questo non sia un punto di arrivo, ma di partenza per future e più profonde considerazioni.
Per una mia predisposizione, quando gli argomenti si fanno tosti e difficili da seguire, ci inserisco delle battutine, delle stupidaggini solo per sdrammatizzare e per alleggerire il discorso, non me ne abbiate.
PREMESSA
Prima di iniziare a teorizzare delle formule occorre necessariamente sapere di cosa stiamo parlando. Il carbonio, elemento essenziale per la costruzione delle canne da pesca, è l’elemento chimico contrassegnato dalla lettera C, cosa importante è un non metallo, quindi ha le proprietà fisiche e chimiche dei non metalli.
Altra considerazione importante da fare è che il carbonio può avere, a seconda della configurazione degli orbitali atomici (paroloni complicati ma credetemi che è così sulla fiducia), legami con 4 o 3 o 2 atomi. Questo è molto importante perché a seconda di quanti atomi si sono combinati con il carbonio avremo molecole di materiali diversi, con diverse caratteristiche fisiche e chimiche. Importantissimo poi è sottolineare che non tutti i legami atomici sono uguali e a seconda del tipo e del numero di legami avremo materiali più o meno duri e resistenti (non scendo nel dettaglio perché solo di questo si dovrebbe scrivere un libro).
Esistono perciò una grandissima varietà di composti del carbonio, che tra l’altro si lega benissimo con molti altri elementi come l’ossigeno(
 ) e l’idrogeno (
) e l’idrogeno ( un tipo di zucchero), ovviamente la parte di applicazione del carbonio che interessa a noi è quella strettamente legata al materiale come elemento costruttivo delle canne da pesca, che nello specifico è la grafite.
un tipo di zucchero), ovviamente la parte di applicazione del carbonio che interessa a noi è quella strettamente legata al materiale come elemento costruttivo delle canne da pesca, che nello specifico è la grafite.In natura la grafite ha due configurazioni la cosiddetta alfa e beta, la prima ha una struttura esagonale, la seconda romboidale, nelle grafite industriali si riscontrano solo le strutture alfa. La grafite ha la caratteristica di essere formata da più fogli di atomi che sono separati da diversi altri atomi che, nel caso funzionino da collante, hanno strutture e forze tali da tenere attaccati i fogli, gli stessi hanno la tendenza a scivolare gli uni sugli altri.
Avete mai notato in caso di rottura di una canna da pesca, sembra che si squami perdendo via via pezzetti sottili di materiale che si sfalda. Ovviamente bisogna considerare che l’industria ha messo a punto sistemi di trattamento meccanico in grado di variare la struttura della grafite (da alfa a beta) e l’aggiunta di altri elementi di rinforzo come il Kevlar consente di avere materiali con diverse caratteristiche meccaniche. Classificare e stabilire per tutte le strutture a base di carbonio utilizzate per la pesca, le caratteristiche fisiche è una utopia perché molti materiali sono coperti da brevetti e la varietà è tale da rendere l’impresa ardua.
DEFINIZIONI PRELIMINARI
Per capire meglio il discorso, per la verità un po’ complicato che andremo a fare di seguito dobbiamo porre alcuni punti saldi da cui iniziare. Prendiamo un elemento di materiale, nel nostro caso una sezione di canna da pesca, poniamo come
 la lunghezza inziale a riposo dell’elemento campione l sarà invece la lunghezza modificata a causa delle tensioni ora definiamo come:
la lunghezza inziale a riposo dell’elemento campione l sarà invece la lunghezza modificata a causa delle tensioni ora definiamo come:Allungamento:
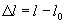
Deformazione lineare epsilonE (teorica):
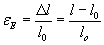
Deformazione lineare epsilonT (reale):

dove ln è logaritmo naturale base e (per chi vuole approfondire l’argomento logaritmi per capire meglio mi scriva pure).
Bisogna inoltre porre in chiaro un concetto: sforzi e deformazioni dipendono inequivocabilmente dal materiale ma sono assolutamente indipendenti dalla forma in cui sono costruiti. Quindi uno studio su una fibra lineare di carbonio permette di avere risultati paragonabili e assimilabili per una canna da pesca oppure per l’alettone di una formula uno.
LE CONDIZIONI DI STUDIO
Una canna da pesca ha la sezione circolare, prendiamo come approssimazione che tale non abbia spina, e che sia perfettamente rotonda.
Prendiamo un elemento della canna:

Durante le sollecitazione dovute al lancio la struttura si deforma

Un lato subisce uno stiramento e la sua lunghezza aumenta di +dl, mentre dall’altra parte il lato subisce una compressione e la sua lunghezza diminuisce di un –dl. Nello specifico selezionando un elemento da entrambi i lati avremo questa situazione:

Ora che abbiamo posto le basi per il nostro studio possiamo immaginare di mettere il nostro campione in una speciale macchina che provvederà a mettere in tensione il materiale, questo ci permetterà di studiare il comportamento del materiale sotto tensione nel lato in cui avviene lo stiramento. Come detto in precedenza lo sforzo e la deformazione sono indipendenti dalla forma del materiale e quindi possiamo studiare la fibra lineare che viene messa in trazione da uno sforzo progressivo e quindi si stira.

Nel grafico Y è il valore della massima tensione ammissibile prima di passare al comportamento plastico. A0 è l’area iniziale della sezione del nostro elemento.
Interpretando il grafico sopra illustrato abbiamo i vari stadi in cui possiamo dividere il materiale durante la prova di tensione.
1) il materiale si allunga all’interno del range di valori in cui ha deformazioni elastiche interrompendo la tensione il materiale torna al suo originale stadio.
2) Passando al di là della soglia di plasticità il materiale continua ad allungarsi in modo uniforme, senza cioè subire significative variazioni di volume. Nello specifico, interrompendo la tensione il materiale tornerebbe alla sua posizione iniziale avendo però delle deformazioni plastiche mantenendo comunque un comportamento elastico

3) proseguendo oltre con la tensione il materiale viene stirato e in un punto, solitamente verso il centro, il materiale forma un collo in cui c’è variazione di superficie dell’area considerata. In questo punto il materiale, analogamente al punto 2 ha un comportamento elastico ma deformazioni plastiche. Importante è notare che, sia nella fase 2 che nella 3, in rapporto alla tensione applicata all’inizio, basta un lieve aumento della tensione stessa per provocare significative deformazioni. Nell’applicazione pratica della pesca, la canna quando raggiunge il limite della tensione elastica/plastica, la canna non ha praticamente deformazioni (vedremo in seguito si dice comportamento anelastico), superando il limite, cioè allungando il lancio e aumentando le forze in azioni, la canna ha deformazioni sensibili anche con leggeri aumenti (da 20 a 21 mt di coda per intenderci).
Altra considerazione da fare su questa fase è che il materiale, come si evince dalla cupside del grafico ha un punto di massimo, tale rappresenta la massima tensione sopportabile dal materiale; per materiali fragili in questo punto si ha rottura, per i materiali duttili vi è la diminuzione della sezione già descritta in precedenza.
4) Proseguendo ancora c’è la rottura che avviene sempre nella zona del materiale che ha subito lo stiramento con la conseguente variazione di area.
Ultima considerazione sul grafico della ipotetica prova è che i materiali hanno un comportamento elastico lineare entro particolari range di deformazioni, ed assumere comportamenti non lineari per valori più elevati. Ovviamente si possono studiare le deformazioni e le tensioni nel campo lineare, quando non sussiste più la linearità delle deformazioni entrano in campo altre variabili (la composizione del materiale, la temperatura, il tempo di esposizione alla tensione) ed è praticamente impossibile determinare il comportamento se non al limite per materiali puri.
MATEMATICA E FISICA
Andiamo ora a condire le considerazioni con un po’ di matematica e fisica per capire effettivamente come e dove succedono le cose appena descritte
Ricapitolando brevemente dobbiamo andare a studiare quelle che sono le deformazioni dovute alle sollecitazioni che per semplicità di comprensione andremo ad assumere infinitesimali andando a studiare un allungamento rettilineo.
Dobbiamo inoltre porre anche altre condizione a contorno:
1) definiamo come solido elastico un elemento che ha la capacità di riacquistare la sua forma iniziale appena scompaiono le forze applicate
2) immaginiamo di avere una tensione uniforme e distribuita uniformemente
La tensione applicata T=F/A cioè la forza su unità di area e la deformazione come
 cioè il rapporto tra l’allungamento misurato e la lunghezza originaria.
cioè il rapporto tra l’allungamento misurato e la lunghezza originaria.Da qui possiamo arrivare a formulare semplicemente che:
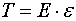
dove T è la forza applicata E è la costante di proporzionalità, che nel mondo intero è conosciuta come modulo di Young (ne parleremo dopo), mentre
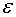 è la deformazione.
è la deformazione.A seconda del materiale e quindi del relativo modulo di Young possiamo stabile la T limite per la deformazione, tale rappresenta nella pratica la soglia oltre cui il comportamento non è più elastica.
Per dare un’idea il modulo di Young per le fibre di carbonio è compresa tra i 275 e i 415 Gpa, per la fibra di vetro è tra i 73 e gli 85 Gpa, per l’acciaio è tra 190 e 200 Gpa, il diamante ha un modulo di Young tra gli 820 e i 1050 Gpa.
Abbiamo quindi definito T, cioè il limite elastico, oltre a questo limite si nota comunque un incremento della deformazione anche senza aumento della tensione ed è il cosiddetto limite di snervamento. Crescendo ulteriormente si notano deformazioni significative fino al limite di rottura e la conseguente rottura del campione.
Ora lo studio del comportamento meccanico dei solidi elastici ha animato i sogni di parecchi matematici e fisici dal XXVII secolo ed in particolare di un fisico/matematico di nome HOOKE che suggerì una generalizzazione proposta già precedentemente da CAUCHY. La differenza sostanziale tra i due era che Hooke conduceva una vita ben più animata, amava infatti il bere il mangiare e soprattutto le donne e questa spensieratezza lo rendeva un pelino più brillante per quei tempi soprattutto per quanto concerne le applicazioni pratiche della sue intuizioni. Cauchy invece faceva una vita triste, e quindi era un grande astrattista specie nella matematica ma quanto al resto pare non avesse successo con le donne e quindi era attanagliato da una grande miopia.
Hooke propose la seguente generalizzazione partendo da una serie di assiomi:
1) lo stato di tensione è funzione univoca dello stato di deformazione, il che si traduce in:

2) le componeti di tensione T si annullano identicamente se sono nulle tutte le componenti di deformazione
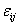 il che implica che nelle condizioni iniziali non è soggetto alcuno stato di tensione
il che implica che nelle condizioni iniziali non è soggetto alcuno stato di tensione3) la funzione f non dipendono esplicitamente dalla posizione x, quindi in materiale è omogeneamente elastico cioè in ogni punto l’elasticità è la stessa
4) il legame
 dove (i,j,k,l=1,2,3) è un legame lineare.
dove (i,j,k,l=1,2,3) è un legame lineare.Ora, la combinazione dei coefficienti
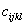 sono 3 alla quarta e quindi 81, risparmiandovi la dimostrazione fidatevi se vi dico che nella realtà ne bastano 36 se si tiene conto della simmetria del tensore T, fidatevi inoltre se vi dico che si riducono ulteriormente a 21 se parliamo di un solido omogeneo anisotropo.
sono 3 alla quarta e quindi 81, risparmiandovi la dimostrazione fidatevi se vi dico che nella realtà ne bastano 36 se si tiene conto della simmetria del tensore T, fidatevi inoltre se vi dico che si riducono ulteriormente a 21 se parliamo di un solido omogeneo anisotropo.Quindi dovremmo in pratica conoscere 21 costanti elastiche (c) per definire 6 tensori di sforzo in grado di descrivere il comportamento elastico, vi scrivo solo il primo:
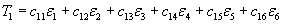
Quindi si andranno di seguito a costruire 6 tensori, da 1 a 6 in cui saranno considerate tutte le costanti elastiche dei vari punti per le relative deformazioni epsilon.
La domanda che sorge spontanea è perché 6 tensori? Allora dobbiamo considerare di avere tre sforzi normali lungo gli assi x,y,z più tre sforzi di taglio xy,xz,yz, questi sei tensori ci danno la gamma completa degli sforzi applicabili.
Semplifichiamo un po’ le cose per renderle leggibili; quella che vi ho enunciato in precedenza è la legge di Hooke nella sua funzione generale e nel suo più ampio spettro di utilizzo. Ovviamente, per le nostre applicazioni non ha senso andare a studiare un numero di tensori così ampio ed andare alla ricerca sperimentale delle costanti elastiche, meglio applicare una ulteriore semplificazione introducendo la legge di Hooke coadiuvata dal modulo di Young.
Non vi dico niente sulla vita di Young, vi dico solo di non confonderlo con Paul Young che è un cantante degli anni ottanta tramontato ormai da tempo e conosciuto in Italia per un duetto con Zucchero nella reinterpretazione di “Senza una donna”.
Seriamente la legge di Hooke diventa molto semplicemente:
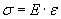
Tutta un’altra cosa,
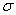 (sigma) è lo sforzo lungo un asse (lo chiamo così per evitare di confonderlo con il T che è un tensore visto in precedenza), E è la pendenza della linea di carico nella fase elastica vista in precedenza (punto 1) ed è caratteristica del materiale, indipendente dalla forma e vale per allungamento e compressione, è la deformazione.
(sigma) è lo sforzo lungo un asse (lo chiamo così per evitare di confonderlo con il T che è un tensore visto in precedenza), E è la pendenza della linea di carico nella fase elastica vista in precedenza (punto 1) ed è caratteristica del materiale, indipendente dalla forma e vale per allungamento e compressione, è la deformazione.La deformazione al livello atomico è data da piccole variazioni della distanza interatomica, il modulo elastico E, o modulo di Young, altro non è che la misura della forza di legame ed è per questo che è strettamente dipendente dal tipo di materiale ed indipendente dalla forma: la prima è ovvia ogni materiale ha legami chimici propri e diversi e quindi resistenze di legame diverse, la seconda è altrettanto ovvia, a livello atomico che si parli di un canna da pesca o di un foglio di carbonio non si vede la differenza : sono atomi legati tra di loro.
Dobbiamo inserire un ulteriore elemento per riuscire poi a formulare una generalizzazione valida ed è il modulo di Poisson. Due parole su Poisson, francese, che nel 2006 non ha potuto vedere la sua nazionale campione del mondo per due motivi, il primo era già morto da un paio di secoli abbondanti, il secondo perche “siamo noi, siamo noi i campioni del mondo siamo noi”.
Poisson osserva giustamente che per la maggior parte dei materiali ad un allungamento dell’asse x a causa di una trazione corrisponde un aumento di volume. Nel caso di deformazione elastica questo è compensato da una contrazione laterale lungo y e z in perpendicolarità con x. Quindi:
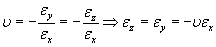
Tanto per dare due numeri
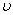 (upsilon = costante di Poisson) per le gomme vale 0,5, per i metalli 0,35 per i materiali ceramici 0.07-0.27. Applicandolo il modulo di Poisson per dedurre uno sforzo applicato lungo l’asse x avremo:
(upsilon = costante di Poisson) per le gomme vale 0,5, per i metalli 0,35 per i materiali ceramici 0.07-0.27. Applicandolo il modulo di Poisson per dedurre uno sforzo applicato lungo l’asse x avremo:
questo ci dà una relazione lineare tra sforzo applicato e deformazione laterale
Ora proviamo ad applicare questa semplificazione di Hooke, supponiamo un corpo sollecitato da un generico stato di sforzo, come abbiamo visto in precedenza per descrivere compiutamente il tutto dovremmo disporre di 6 equazioni, tre per gli assi e tre per gli sforzi di taglio. Consideriamo per semplicità i soli sforzi agenti lungo gli assi x, y e z, trascurando quelli di taglio.
L’applicazione di tali sforzi genererà anche una conseguente contrazione (Poisson) avremo quindi che la componente dello sforzo
 genera una
genera una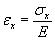 e le conseguenti deformazioni quantificabili con Poisson nelle direzioni y e z
e le conseguenti deformazioni quantificabili con Poisson nelle direzioni y e z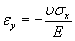 e
e 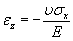 .
.La stessa cosa ovviamente si avrà prendendo in considerazione
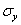 e
e  .
.La deformazione totale lungo l’asse delle x sarà:

Quindi nei tre assi avremo le seguenti deformazioni:
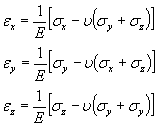
Come un miracolo della matematica abbiamo ridotto le equazioni a tre con due moduli elastici (dipendenti dal tipo di materiale) E e
 al posto di avere 6 equazioni con la bellezza di 36 costanti elastiche da calcolare (di cui solo 21 indipendenti).
al posto di avere 6 equazioni con la bellezza di 36 costanti elastiche da calcolare (di cui solo 21 indipendenti).Questo ci permette di calcolare puntualmente le deformazioni che si osservano in ciascuna direzione per uno sforzo assegnato
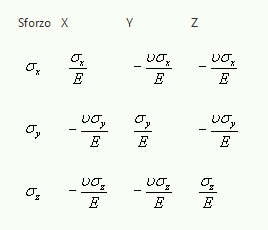
Ora facciamo il punto della situazione, abbiamo capito che i materiali danno diverse risposte alle sollecitazioni, a seconda degli sforzi assegnati si hanno delle deformazioni che possiamo calcolare partendo dai moduli elastici. Tutto questo è valido solo nel campo delle forze entro cui si hanno deformazioni elastiche (nello specifico prima delle tensioni di snervamento).
Analizziamo adesso i casi in cui si ha un comportamento anelastico e non lineare. Per farlo dobbiamo per forza di cose fare un viaggio all’interno della struttura molecolare del materiale. Immaginiamo il materiale come un agglomerato ordinato di paline (gli atomi) legati gli uni agli altri da delle molle. La forza di ritrazione (cioè la forza per tornare alla posizione iniziale) è indotto dallo spostamento degli atomi.
Per materiali come metalli, ceramici, vetri e polimeri la forza di ritrazione deriva da piccoli spostamenti degli atomi dalla loro posizione di equilibrio. Questi materiali sono dotati di una grande forza di coesione e quindi la forza di ritrazione è alta, il modulo elastico pure e le deformazioni sono limitate e associate ad un significativo aumento dell’energia interna mentre la configurazione solida (il reticolo di palline con le molle) risulta sempre inalterata.
Negli elastomeri (polimeri plastici sia naturali, che sintetici con grandi capacità elastiche) la struttura tridimensionale assicura la reversibilità delle deformazioni perché a spostarsi sono segmenti di catena di elastomeri (con forza di ritrazione alta) mentre tra le catene c’è una bassa forza di ritrazione. In altre parole le catene molecolari degli elastomeri sono dure e rigide ma tra loro sono debolmente legati. Esempio lampante di elastomero è la gomma, l’allungamento a trazione è molto ampio ma a muoversi non è il singolo atomo bensì la catena di atomi.
In alcuni casi possono osservare comportamenti anelastici, cioè la risposta del materiale in fase di carico e scarico non è lineare. Nella deformazione elastica ideale l’energia immagazzinata viene totalmente recuperata alla rimozione del carico, nel caso di comportamento anelastico una parte dell’energia di deformazione viene dissipata nel materiale attraverso meccanismi di attrito interno che si traduce in un movimento di dislocazione delle catene molecolari. La curva di scarico non è più uguale a quella di carico anche se il campione riassume la forma iniziale. Il comportamento anelastico si manifesta come una dipendenza elastica dal tempo che può essere osservata applicando uno sforzo costante ad un provino per un certo tempo e osservando come varia la deformazione nel tempo.
Tanto per citare due esempi di materiale con conclamato e visibile comportamento anelastico abbiamo la ghisa grigia, in cui l’effetto anelastico è dovuto ai movimenti di dislocazione delle lamelle di grafite inserite nella matrice di ferro, altro esempio sono i pneumatici, formati essenzialmente da elastomeri che rispondono alle tensioni con un attrito interno. Importante è notare che questi due materiali sono dei grandissimi ammortizzatori di vibrazioni.
CONCLUSIONI
In conclusione, tiriamo le somme definitive di questo lungo e complesso discorso cercando di capire cosa succede in una canna da pesca. Le canne da PAM, vendono sottoposte a continue sollecitazioni in tutti e tre gli assi. Con le formule che abbiamo visto possiamo determinare a priori (a patto ci conoscere le caratteristiche meccaniche dello specifico materiale composito) la tensione massima applicabile prima di raggiungere lo snervamento, le deformazioni sui tre assi attese a seconda delle forze applicate in modo abbastanza semplice.
Abbiamo inoltre visto che i materiali possono avere un comportamento anelastico, cioè facendo un lancio particolarmente oneroso in termini di tensioni, la risposta della canna non è più elastica e quindi non restituisce l’energia applicata non lavorando. Quando questo capita siamo già oltre il livello di tensione di snervamento e quindi, aumentando ulteriormente avremo delle deformazioni maggiori anche applicando piccole differenze di tensione (ad esempio passando da 20 a 21 metri di coda in aria, la tensione applicata in più è poca ma le deformazioni saranno maggiori) queste restituiranno una maggiore energia tale da superare il comportamento anelastico. Questo succede perché le catene molecolari che compongono il materiale si dislocano cercando una nuova dimensione spaziale perché nelle catene c’è una grande forza di coesione ma tra di loro le catene non sono legate da una grande forza.
Quindi questo spiega il comportamento sordo di certe canne in particolari stati di deformazione.
Non ho scoperto niente, né ho inventato o teorizzato qualcosa di nuovo, ho solo raccolto le nozioni necessarie e cercato di tradurle in un modo comprensibile e tale da fornire una spiegazione spero esauriente. Se avete notato qualche errore o omissione scrivetemi, se vi sembra che abbia scritto cose sbagliate scrivetemi saranno tutte ben accette.
Fongaro Matteo
Questo indirizzo email è protetto dagli spambots. È necessario abilitare JavaScript per vederlo.
Questo indirizzo email è protetto dagli spambots. È necessario abilitare JavaScript per vederlo.
© PIPAM.org















 Luglio 2009
Luglio 2009