PARTE PRIMA Questo lavoro nasce da un intervento di Ghost su quello straordinario luogo di scambio di idee ed esperienze pam che è il forum di Pipam.
Era alla ricerca di un metodo per trasformare una canna in bamboo a sezione esagonale piena in una “hollow built” ossia cava, mantenendo le caratteristiche di potenza e di azione di quella originaria.
Sollecitato dall’intervento di Ghost ho cominciato a cercare sui forum USA e nei siti specializzati, ma non sono riuscito a trovare molto sull’argomento e quel poco mi è sembrato piuttosto empirico, spesso contraddittorio e, talvolta, privo di qualunque fondamento: perciò ho pensato di elaborare un possible metodo di calcolo che potesse orientare le scelte del rodmakers che volesse trasformare in cava la sua canna piena preferita.
Si tratta pur sempre di un calcolo approssimato e certamente non pretendo di risolvere il problema in modo esatto, ma solo di fornire una base di partenza per le prove di costruzione che, secondo me, sono in ogni caso indispensabili.
Premetto subito,infatti, che condivido il pensiero di J. Gierach che ad un certo punto del suo straordinario libro “Fishing bamboo”, afferma: computers don’t fish.
Se è vero che il calcolo da solo non è sufficiente a determinare un buon taper per una canna che possieda le caratteristiche ricercate in fatto di prestazioni, azione, e piacevolezza d’uso, e che l’esperienza e “l’arte” del rodmaker è insostituibile, è però altrettanto vero che l’approccio analitico risulta assai utile per individuare la strada da seguire per i nostri tentativi, ridurne il numero ed interpretare i risultati ottenuti.
Il problema principale in questi casi è che, giocoforza, occorre far ricorso a nozioni matematiche e fisiche, e si finisce per riempire qualche pagina di calcoli che quasi nessuno ha la voglia di seguire e poi di applicare.
Ed invece quello che alla fine conta veramente è produrre un qualcosa che sia effettivamente utilizzabile da chiunque ne abbia interesse.
Per fortuna, il mitico GHOST ha elaborato un foglio di calcolo in Excel che rende rapido ed alla portata di tutti il calcolo da me impostato, che altrimenti avrebbe rischiato di non avere alcuna utilità pratica.
Col foglio di calcolo davanti, si opera in questo modo.
Si indica un nome per la canna (il foglio è pre-caricato con i dati della Dickerson 8013)
Nel riquadro in alto “parametri” si inserisce la prima stazione della P.F. dalla quale si vuole iniziare a svuotare la canna.
Subito sotto si inserisce il Coefficiente di Svuotamento: se decidiamo di togliere il 60% dell’altezza dello strip, lasciando quindi uno spessore di parete del 40%, il coefficiente di svuotamento sarà 0,6 e così via (vedi definizione più sotto).
I parametri Impact factor e Peso Specifico possono essere lasciati come sono, il Coefficiente Diaframmi, che tiene conto dei diaframmi pieni lasciati lungo gli strip, può esser variato in base alla percentuale di bamboo che si desidera svuotare.
Nella colonna 2 (numeri rossi) si inseriscono le Dimensioni in pollici della canna a sezione piena che si vuole riprodurre cava.
Nella colonna 3 (numeri rossi) si inseriscono i valori del Momento Totale per la canna a sezione piena, prelevandoli da Hexrod
http://www.uwm.edu/~stetzer/Tapers/index.html dalla colonna “total” della sezione “detailed Numbers”.
Nella terz’ultima e penultima colonna a destra si leggono rispettivamente i nuovi diametri in pollici della canna cava ed il valore di settaggio della p.f. in mm.
Tutto qui: il nuovo taper è calcolato ed il rodmaker può passare alla fase realizzativa. Il resto dell’articolo dove sono illustrati i principi e lo sviluppo dettagliato dei calcoli può essere tranquillamente saltato.
La canna cava così calcolata avrà lo stesso ”feeling” di quella piena originale? Chi lo sa, l’unico modo è costruirle tutte e due e provarle.
Spero che sia di aiuto a qualcuno.
Per scaricare lo zip del foglio excel (circa 1 Mbyte) [cliccare quà] salvarlo e decomprimerlo sul proprio PC Il foglio contiene delle operazioni ripetitive che utilizzano delle variabili, quindi prima di aprire il foglio, in Excel occorre controllare ed eventualmente impostare, con (Strumenti – Opzioni – Protezione), l’opzione di Protezione Macro sul livello Media. Aprendo il foglio, apparirà la richiesta di conferma Avviso di protezione, scegliere "Attiva Macro" PARTE SECONDA (altamente cosigliata a chi soffre d’insonnia)
Prendiamo in considerazione una sezione generica di una canna esagonale piena formata da sei triangoli equilateri (strip) di altezza H.
Le caratteristiche della sezione sono:
Area Ap = 6H
2 /
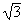
Momento d’inerzia Jp = 5H
4 / 3
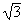
Modulo di resistenza wp = 5H
3 / 3
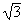
La massa della sezione e quindi il peso è legato all’area della sezione, mentre la rigidità alla flessione (o se vuoi la deformazione della canna) è legata al momento d’inerzia.
Lo sforzo (tensione) nel materiale (bamboo) è invece legato al modulo di resistenza.

Definiamo fattore di “svuotamento” il rapporto tra la parte di vertice di ogni strip da rimuovere e la semi-altezza della sezione , cioè s=h/H.
Ciò significa che un fattore s=0 corrisponde alla sezione piena, un fattore 0,25 corrisponde ad uno spessore di parete di tre quarti della altezza originaria dello strip ed un fattore di 0,50 corrisponde ad uno spessore di parete di metà dell’altezza originaria dello strip.
Se ad esempio riduciamo l’altezza dello strip alla metà, cioè s= 0,5 l’area della sezione e quindi il peso, varierà in funzione del quadrato di H e quindi di 0,5
2 = 0,25 cioè a dire risulterà ridotta del 25%.
La rigidezza alla flessione verierà in funzione della quarta potenza di H ovvero risulterà ridotta dello 0,5
4 = 0,0625 e cioè del 6,25%; infine la resistenza varierà in funzione della terza potenza di H e quindi risulterà ridotta del 12,5%.
Prima considerazione:
Non è possibile determinare una sezione esagonale hollow che abbia le stesse caratteristiche di resistenza (modulo di resistenza) e di deformazione (momento d’inerzia) della sezione esagonale piena. Occorrerebbe variare la geometria della sezione passando dall’esagono regolare ad un poligono di forma più complessa.
Vale a dire che passando da una canna esagonale piena ad una hollow, dobbiamo scegiere se mantenere inalterata la deformabilità della canna piena originaria, oppure la tensione nel bamboo (Garrison stress), ma non possiamo avere contemporaneamente soddisfatte tutte e due le condizioni.
Ne consegue che se manteniamo inalterato il diagramma delle tensioni (come fanno quasi tutti i programmi di “rod design” in circolazione) la porzione di canna svuotata risulterà più rigida della originaria piena.
Ora, a me sembra che il fattore maggiormente rilevante per determinare l’azione di una canna sia rappresentato dalla deformazione che questa assume durante l’azione di lancio; e di conseguenza, dovremmo far sì che la sezione hollow abbia lo stesso momento d’inerzia di quella piena, perchè la deformazione della canna è legata appunto, al momento d’inerzia della sezione (oltre che alla lunghezza che però non viene variata, ed al peso di cui ci occuperemo dopo).
Per avere lo stesso momento d’inerzia della sezione piena, quella cava avente fattore di svuotamento s, dovrà avere un’altezza Hc =

In pratica si sceglie da quale sezione iniziare lo svuotamento, si sceglie quanto togliere dello strip cioè il fattore s, e si trova l’altezza di questa prima sezione moltiplicando l’altezza della sezione piena originaria per il coefficiente
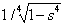
Esempio pratico:
Supponiamo di voler trasformare in hollow built una canna piena di cui conosciamo il taper iniziando a svuotare dalla sezione 50 e che questa misuri 0,200”.
Decidiamo di togliere il 60% dell’altezza dello strip, lasciando uno spessore di parete del 40% perciò s= 0,6.
L’altezza della sezione cava sarà:
0.200 x
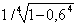
= 0.200 x 1,03531= 0,207”
cioè l’altezza della sezione deve essere aumentata del 3,53% per compensare la diminuzione di rigidezza dovuto allo svuotamento del 60%.
Se poniamo k =
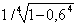
abbiamo la semplice formula:
Hc = k x Hp
In pratica basta moltiplicare la misura della sezione del taper pieno originale per il k relativo allo svuotamento s prescelto e si trova la misura della sezione cava avente lo stesso momento d’inerzia di quella piena.
Naturalmente i valori di k possono essere calcolati una volta per tutte per quei fattori di svuotamento che interessano nella pratica.
per s = 0,40 k = 1,0065
per s = 0,45 k = 1,0105
per s = 0,50 k = 1,0162
per s = 0,55 k = 1,0243
per s = 0,60 k = 1,0353
per s = 0,65 k = 1,0504
e così via.
Semplice no?
Troppo direi, infatti il calcolo è corretto solo per la prima sezione, quella in corrispondenza della stazione dalla quale vogliamo iniziare a svuotare (nell’esempio la 50”).
Per le successive sezioni dovremo ridurre progressivamente questo aumento percentuale per tener conto del fatto che il minor peso del bamboo dovuto allo svuotamento indurrà minori sollecitazioni nella canna.
Altrimenti la canna risulterà un pò più rigida nella parte cava rispetto al taper originale.
Dovremo quindi calcolare il momento flettente nelle stazioni successive che risulterà un poco minore di quello del taper originale ed in proporzione ridurre il momento d’inerzia della sezione.
Per far le cose più semplici possibile, potremo usare Hexrod dove per ogni stazione vengono calcolati i momenti flettenti dovuti alle varie componenti di carico (statiche), ed il momento totale.
Quindi non dovremo rifare tutti i calcoli dei momenti ma solo quelli dovuti al bamboo asportato; sottraendo questa quantità dal momento totale troveremo il valore del momento per la nuova canna cava e dividendolo per il momento totale della canna piena, avremo il coefficiente riduttivo cercato.
Chiamando d
50 la misura della canna piena alla stazione 50 (d=2Hp) avremo:
Av
50= 0,866
. k
2S
2. d
502 area della parte di bamboo asportato alla stazione 50
Av
55= 0,866
. k
2S
2. d
552 area della parte di bamboo asportato alla stazione 55
Il volume del prisma risulterà:
V= 5/3
. ( Av
50 + Av
55 + (Av
50 . Av
55)
1/2) =
=1,667
. 0,866
. k
2S
2 . (d
502 + d
552+ (d
502 . d
552)
1/2)
Assumendo (come Garrison) il peso specifico del bamboo 0,668 oz/cu.in. si ha che il peso del bamboo asportato tra la stazione 50 e la 55 è:
P
55=0,964
. k
2S
2 . (d
502 + d
552 + (d
502 . d
552)
1/2)
ed il momento alla stazione 55 dovuto alla parte di bamboo asportata risulta:
Mv
55= 4
. P
55 . L
55 Il fattore 4 è quello che Garrison chiama “impact factor” in pratica un coefficiente amplificativo per tener conto degli effetti del carico dinamico rispetto a quello statico, e che viene usato anche in Hexrod.
L
55 è la distanza tra la stazione 55 ed il baricentro del bamboo asportato tra la stazione 50 e la stazione 55 e vale:
L
55 = 5/4( 3Av
50 + Av
55 + 2
. ( Av
50 . Av
55)
1/2) / ( Av
50 + Av
55 + (Av
50 . Av
55)
1/2)
e cioè:
L
55 = 1,25
. (3d
502 + d
552 + 2
. (d
502 . d
552)
1/2) / (d
502 + d
552 + (d
502 . d
552)
1/2)
Mt
55 è il momento totale della canna piena alla stazione 55 (preso da Hexrod) Mt
55 - Mv
55 è il momento totale della nuova canna cava alla stazione 55
Quindi f
55 = (Mt
55 - Mv
55 ) / Mt
55 è il coefficiente che cercavamo.
Il momento d’inerzia alla stazione 55 della canna cava dovrà essere uguale al momento d’inerzia della canna piena moltiplicato per f.
Ovvero Hc
554 = f
. k
4 . Hp
554 Quindi la misura della sezione cava alla stazione 55 sarà:
Hc
55 =
 55 .
55 . k
. Hp
55 Per la stazione successiva, la 60, avremo:
P
60 = 0,964
. k
2S
2 . (d
552 + d
602 + (d
552 . d
602)
1/2)
L
60 = 1,25
. (3d
552 + d
602 + 2
. (d
552 . d
602)
1/2) / (d
552 + d
602 + (d
552 . d
602)
1/2)
Mv
60 = 4P
55 . (L
55 + 5) + 4L
60 . P
60 f
60 = (Mt
60 - Mv
60) / Mt
60 Hc
60 =
 60 .
60 . k
. Hp
60 Per la stazione 65 avremo:
P65 = 0,964
. k
2S
2 . (d
602 + d
652 + (d
602 . d
652)
1/2)
L
60 = 1,25
. (3d
602 + d
652 + 2
. (d
602 . d
652)
1/2) / (d
602 + d
652 + (d
602 . d
652)
1/2)
Mv
65 = 4P
55 . (L
55 + 10)+ 4P
60 . (L
60 + 5)+ 4L
65 . P
65 f
65 = (Mt
65 - Mv
65) / Mt
65 Hc
65 =
 65 .
65 . k
. Hp
65 Per la stazione 70 avremo:
P
65 = 0,964
. k
2S
2 . (d
652 + d
702 + (d
652 . d
702)
1/2)
L
60 = 1,25
. (3d
652 + d
702 + 2
. (d
652 . d
702)
1/2) / (d
652 + d
702 + (d
652 . d
702)
1/2)
Mv
70 = 4P
55 . (L
55 + 15)+ 4P
60 . (L
60 + 10)+ 4P
65 . (L
60 + 5)+ 4L
70 . P
70 F
70 = (Mt
70 - Mv
70) / Mt
70 Hc
70 =
 70 .
70 . k
. Hp
70 e così via.
Per conoscere il peso in once del bamboo asportato si esegue la somma:
P
50 + P
55 + P
60 ……
I risultati sono opportunamente moltiplicati per un coefficiente (ad esempio 0,8) per tener conto dei diaframmi pieni lasciati.












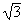
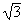










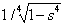


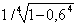 = 0.200 x 1,03531= 0,207”
= 0.200 x 1,03531= 0,207”

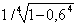





























 55 . k . Hp55
55 . k . Hp55





 60 . k . Hp60
60 . k . Hp60





 65 . k . Hp65
65 . k . Hp65





 70 . k . Hp70
70 . k . Hp70





















 Aprile 2008
Aprile 2008